私がよく読む本の中に「リーン・スタートアップ」という本があります。
教育系ベンチャーの創業者の方からの紹介で購入しました。
まずはその本の紹介をします。
製品開発でよくありがちな失敗として以下のようなものがあります。
自分たちの想像だけで製品の全ての機能を完成させてしまい、それを一気に売りに出したのだが全く売れなかった。
改修をかけようにも機能が多すぎて、完成品のどの機能が顧客に受け入れられている・いないかがわからない。
改修のポイントを掴めたとしても、かなり完成した製品なので改修する工数がありすぎて、時間的にも金銭的にもものすごい負荷がかかってしまう。
このようなことを避けるための方法や考え方が、「リーン・スタートアップ」には記されております。要約すると以下のようになります。
まずは必要最低限の機能だけを作って世の中に出し、顧客との対話を繰り返す中で少しづつ機能を増やしていく。
そうすることで、時間的にも金銭的にも無駄のない製品開発ができる。
ここまでが本の紹介です。
ここで中高生に対して質問です。
これって普段の勉強でも同じことが言えないでしょうか?
上記の失敗例を受験勉強に置き換えると、以下のように言えますよね。
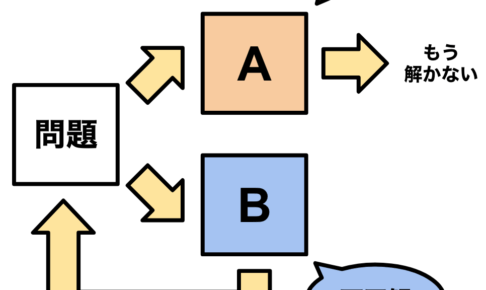
5科目全ての問題集を同時並行で進めてしまったものの、途中で進め方の悪さに気づいたり、今ひとつ成績が伸びなかった。
ある科目で勉強の進め方の悪さに気づいて、他の科目にも活かせそうだと思っても、それが本当に他の科目にも活きるのかがわからないから躊躇する。
仮に他の科目にも活きることがわかり、他の科目の勉強の進め方を変更したとしても、今までやった範囲も同様の勉強法で行わないと理解のムラができるので、全ての範囲をやり直す必要が出てくる。
結果、無駄な勉強時間が増えたり、成長が遅くなる
一方、リーン・スタートアップ的な考え方だと、以下のようになります。
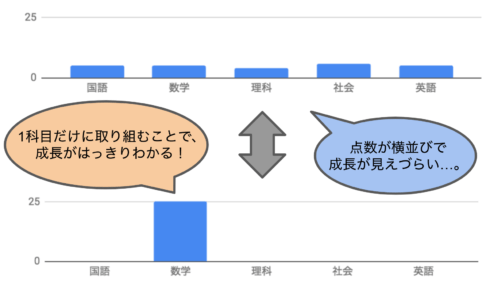
まず1科目を少ない問題集で仕上げる。この間に様々な勉強法を試行錯誤し、自分にあった勉強法を固める。
1科目仕上がったら、別の科目に1科目ずつ着手していく。
1科目仕上げるごとに勉強法がブラッシュアップされ、最後の方の科目は短期間で仕上げられるようになる。
リーン・スタートアップでは試行錯誤の部分を「構築―計測―学習」と説明されておりまして、今回は勉強における「構築―計測―学習」を、大学受験の数学を例に説明していきたいと思います。

想定
- 進学校に通う高校2年生の男子生徒。サッカー部に所属。
- 今までの定期テストはクラスで下の方。模擬試験でもパッとせず、センターの過去問では全科目4~6割程度の得点率。
- 目標だけは高く、志望校は東京大学理科1類。
- 現在は3月で、あと少しで受験生。春休みを機に、まずは数学から本格的な受験勉強を開始。
構築

まずは青チャートの1Aから始めよう。
収録されているのは例題、練習、EXERCISE、総合演習の4つ。
例題は各分野の標準的な問題だから、これをやれば網羅的に全分野を学ぶことができそうだ。
練習とEXERCISEは例題と難易度がほとんど同じで、範囲も被っている。これは一旦外して、例題が終わってから着手するか検討しよう。
総合演習は難易度が例題よりも高めみたいだ。これも例題が終わってから検討しよう。
まずは例題から着手。こちらの記事を参考に行おう。
以下のような時間の見積もりになる。2週間かけて青チャートの例題を行おう。
例題は1A合わせて300題程度。
模範解答を書き写して理解するのに1題あたり6分。300題あるので1,800分、すなわち30時間。
実際に問題を解くのに1題あたり6分。300題のうち半分は間違えるとして、実際に解く延べ問題数は450題。450題あるので2,700分、すなわち45時間。
合計で75時間。
計測

センター数学1Aの過去問を用いて、自分が行なった勉強の成果を定量的に検証しよう。
1月頃に行なったセンター同日体験模試では数学1Aの点数が49点だったが、今回別の年度を解いてみたところ、今回の点数は78点だった。
点数を問題ごとに確認すると、「大問の最初の問題は解けているものの、最後の方の問題で落としている」ということがわかった。
学習

大きく成長することができた。この勉強法は他の分野(数学2B、3)や科目(特に物理や化学)にも活かせそうだ。
一方で、東大を志望するのであれば最低でも9割は欲しい。
そのために、各大問の最後の方の問題までしっかり正答できる必要がある。
解いてみた感想として「大問の最初の方は難なく解けたけど、最後の方は難しくて解けなかった」というのがあった。
9割に到達するために、思いつくアプローチとしては2つ。
- 例題(300題)を全てもう一度解き直す。大問の最後の方の問題以外の解答スピードの向上を望むことができる。
- 総合演習(60題)を解いてみる。大問の最後の方の難しい問題が解けるようになる。
一長一短あるものの
- はかなり時間がかかりそうだ。しかも1回は正解した問題ばかりだから、演習効果が薄い可能性もある。
- は問題数が少なく、すぐにできそうだ。思考の幅を広げることもできそう。
時間対効果的が高いのはおそらく後者なので、総合演習に着手しよう。
これで効果が出れば、「基礎を網羅的に押さえた上で、難易度の高い問題を少ない問題数行えば効率よく点数を伸ばすことができる」という教訓が得られ、他の科目にも活かせそうだ。
最後に
以上が「勉強における『構築―計測―学習』」です。
綿密な計画に基づいて学力を「構築」し、それをテストを用いて数値的に「計測」した後、その数値的計測を基に「学習」し、次の「構築」へと活かす。
このサイクルを回すことで、安定的に点数を伸ばすことができる、自分に合った勉強法を見つけることができるはずです。

















コメントを残す