数学の記述問題が出題される2次試験や私大入試を受験されるみなさん、解答を記述する上でお悩みはございませんか?
高校生のお話を聞いていると、数学の記述について以下の悩みを持っている方が多いように思えます。
- 記述のやり方がわからない。なにを書けば良いのか。なにを書いてはいけないのか。
- 記述に時間がかかる。短縮する方法はないのか。
- 解答用紙の使い方がわからない。無駄なスペースができてしまう。図の配置に迷う。
今回は、これらのお悩みを解決するための記事を書きました。
私は大手予備校の大学別模試の数学の採点経験がございまして、今までに合計で10,000枚以上の解答を採点してきました。加えて、元東大受験生であり、普段から数学の解答の書き方にはこだわって勉強しておりました。
そんな私の考え方として、参考にしてもらえると嬉しいです。
目次
解答用紙には過不足なく記述すること
言い換えると、「必要な解答だけを書き、本筋に関係ない計算などはなるべく書かないようにしましょう」ということです。
解答用紙には必要のないことは書かないこと
受験生の解答を見てみると、本筋に関係のない計算や必要のない証明を書いているものが多く見られます。
例えば式の展開。
(x2 + 2x + 3)(x2 + 4x + 5)を展開する場合、この展開の結果自体が問われるのであれば途中式を書くべきですが、そうでない場合は展開結果のみを書けば大丈夫です。
= x4 + 4x3 + 5x2 + 2x3 + 8x2 + 10x + 3x2 + 12x + 15
= x4 + 6x3 + 16x2 +22x+15
= x4 + 6x3 + 16x2 +22x+15
展開して整理する前の部分(x4 + 4x3 + 5x2 + 2x3 + 8x2 + 10x + 3x2 + 12x + 15)は不要です。展開の結果自体を問われているのでもない限り、採点官としてもどうでもよいからです。
加えて、あまり途中式を書きすぎると解答用紙を圧迫してしまいます。そうなると、あとでスペースが必要になった際に解答を書きなおさなければなりません。
途中式を全く書いてはいけないわけではないですが、その途中式が解答に重要なものでない場合は加点対象となることはなく、解答用紙を圧迫するだけで基本的にメリットはありません。途中式を書くかどうかはよく考えましょう。
あとは、公式の証明。
高校~大学教養課程レベルで広く知れ渡っているものであれば、特に証明することなく利用して大丈夫です。
公式を毎回証明していると、採点官としても読みづらいですし、解答用紙も圧迫します。
こちらも基本的にメリットはないので、証明は省きましょう。
証明が必要なのは以下の3つの場合です。
- その問題で証明自体が問われている場合
- その問題で特有の公式を導入しなければならない場合
例:整数問題などである規則性が読み取れ、その規則性を証明して公式とし、その公式を用いなければ解答できない場合 - その公式が一般的にあまり馴染みがないと考えた場合
※これは個人の感覚によります。普段の勉強の中で、この辺りの感覚は身につけるようにしましょう。迷ったら証明、というスタンスでも良いかもしれません。
必要なことは解答用紙にしっかり書くこと
必要なことを書かなければ点数がこないというのもあるのですが、式を羅列しているだけの解答用紙も多いです。
「1式、2式、3式…」ではなく「1式、すなわち2式、よって3式…」のように、適切に言葉を補うようにしましょう。
式の羅列だけだと、式の関係性や因果関係を構築できているのかが読み取れず、場合によっては減点の対象となります。
その他
上記で挙げたのは、あくまで1例です。
細かいポイントを挙げるとキリがないので、問題集の模範解答から学び取りましょう。
オススメの勉強法は「模範解答の理解と写経」です。
ポイントは写経でして、模範解答を書き写すことで、数学の記述解答で必要な常識や記述解答に適した文体を一気に身につけることができます。
関連記事も参考に、まずは青チャートなどの模範解答の写経から行いましょう。
字は判別できるように書くこと
言い換えると、「字は判別できる範囲でキレイに書きましょう」ということです。
字はキレイに書きましょう
書き殴っているような汚い記述解答を見ることが多いですが、2つ以上に捉えられる字(1と7、tと+、qとg、など)を書くと、それが加点されない場合があります。
紛らわしいものはしっかり区別するようにしましょう。私は受験生の頃、以下のように工夫をしておりました。
- 変数としてtはなるべく使わない。+と混同しやすいため。使わざるを得ない場合はtの下をしっかりはねさせる。
- qはなるべく使わない。ブロック体の場合は9と、筆記体の場合は8やgと混同しやすいため。使わざるを得ない場合は筆記体を使用し、二つの輪っか部分を明確に離すようにする。
- zはブロック体を使う。筆記体のzは筆記体のyと混同しやすいため。
- ブロック体のzの真ん中に点を入れる。2との混同を防ぐため。
- oはなるべく使わないこと。0と混同しやすいため。使わざるを得ない場合はoか0なのかを毎回考える。
- ×(かける)はなるべく使わないこと。Xと混同しやすいため。外積で用いる場合は×(かける)かXなのかを毎回考える。
字は判別できれば大丈夫です
ただ、数学のテストは漢字のテストではないので、判別できれば大丈夫です。
私は受験生の頃、以下のように工夫をして手間と時間を省略しておりました。
- 「数」の字の「米」の部分を「十」と書くなどして画数を減らす。
- 「確率」は「カクリツ」などとカタカナで書く。
※ただし、公式の名前などは漢字で記述するようにする。例えば「三平方の定理」などは「サンヘイホウのテイリ」などとは書かないようにする。公式の名前などは漢字が正式な表記であり、それを崩すと減点の対象となり得るため。 - 「よって」は「∴」、「というのも」は「∵」で代用する。
その他
それ以外に、解答を書く上で、私は以下のように工夫をしておりました。
- 式に番号を割り振る場合、「…③」ではなく「ー③」と書く。「…」だと3画だが「ー」だと1画で済むため。
- 答えを書く場合は「…(答)」などと書かず、下線を一本引くだけにする。
また、式を複数書く場合に、「⇔」を使わないようにしましょう。「⇔」を多用する方が時々いますが、必要十分条件の「⇔」は成り立つのかを厳密に判断されます。成立していなければ減点の対象となるので、必要十分条件を明確に示したい場合以外は「⇔」を使わないようにしましょう。
※このことは「東大数学で1点でも多く取る方法」にも示されております。解答の書き方を学ぶ上でとても良い参考書なので、特に東大受験生にはオススメです。
解答用紙は無駄なく使うこと
無駄な余白があると、解答スペースが足りなくなります。
余白が発生しないようにする工夫として、解答用紙を真ん中で2つに分けるのをオススメします。
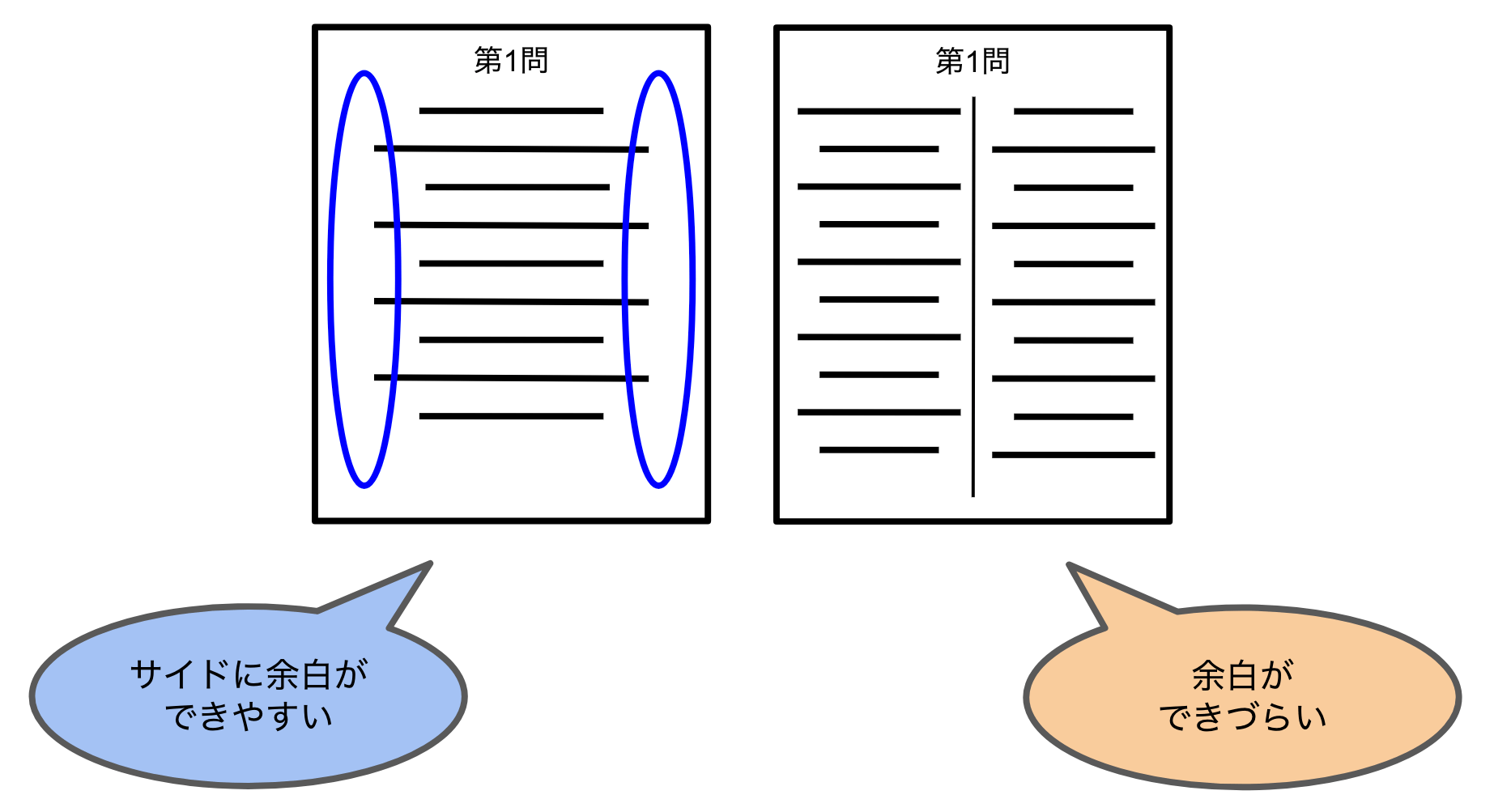

解答用紙を真ん中でわけないと、以下のいずれかのことが起こります。
- 端まで書くと、文の右端と次の文の左端を確認する際に一回視線が分断される。ゆえに、文章の整合性を確かめるのに時間や労力がかかる。
- 端まで書かずに余白を残すと、解答スペースが足りなくなる恐れがある。
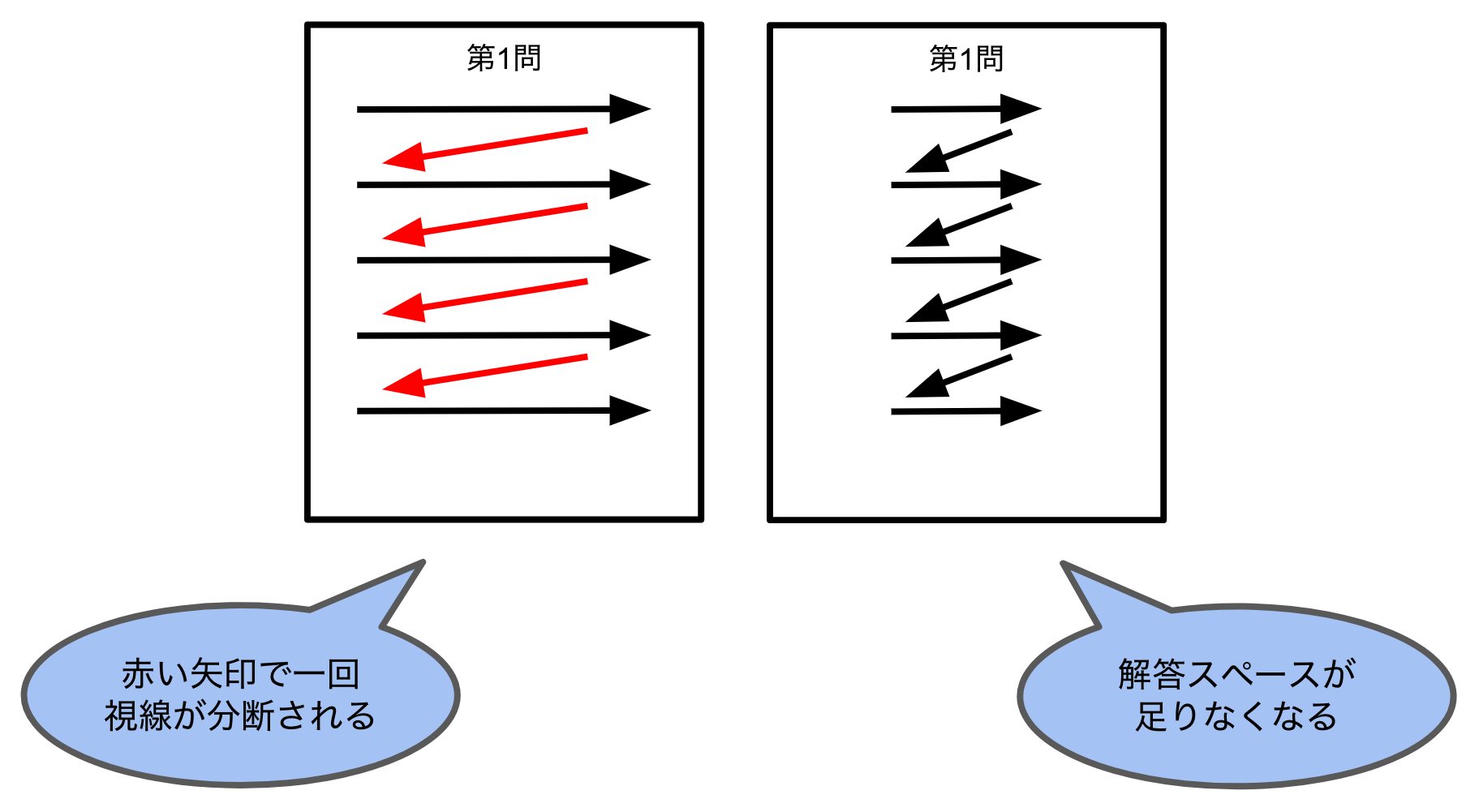

一方で、解答用紙を真ん中で分けると以下のような2つのメリットがあります。
- 余白を残さないように端まで書いても、文の両端とも視野に入る。ゆえに、文章の整合性を確認しやすい。
- 横方向がスマホの横の長さと同じくらいになり、縦方向に流し読みすることもできるようになる。ゆえに見直しがしやすくなる。(これは採点官にとっても助かります。)
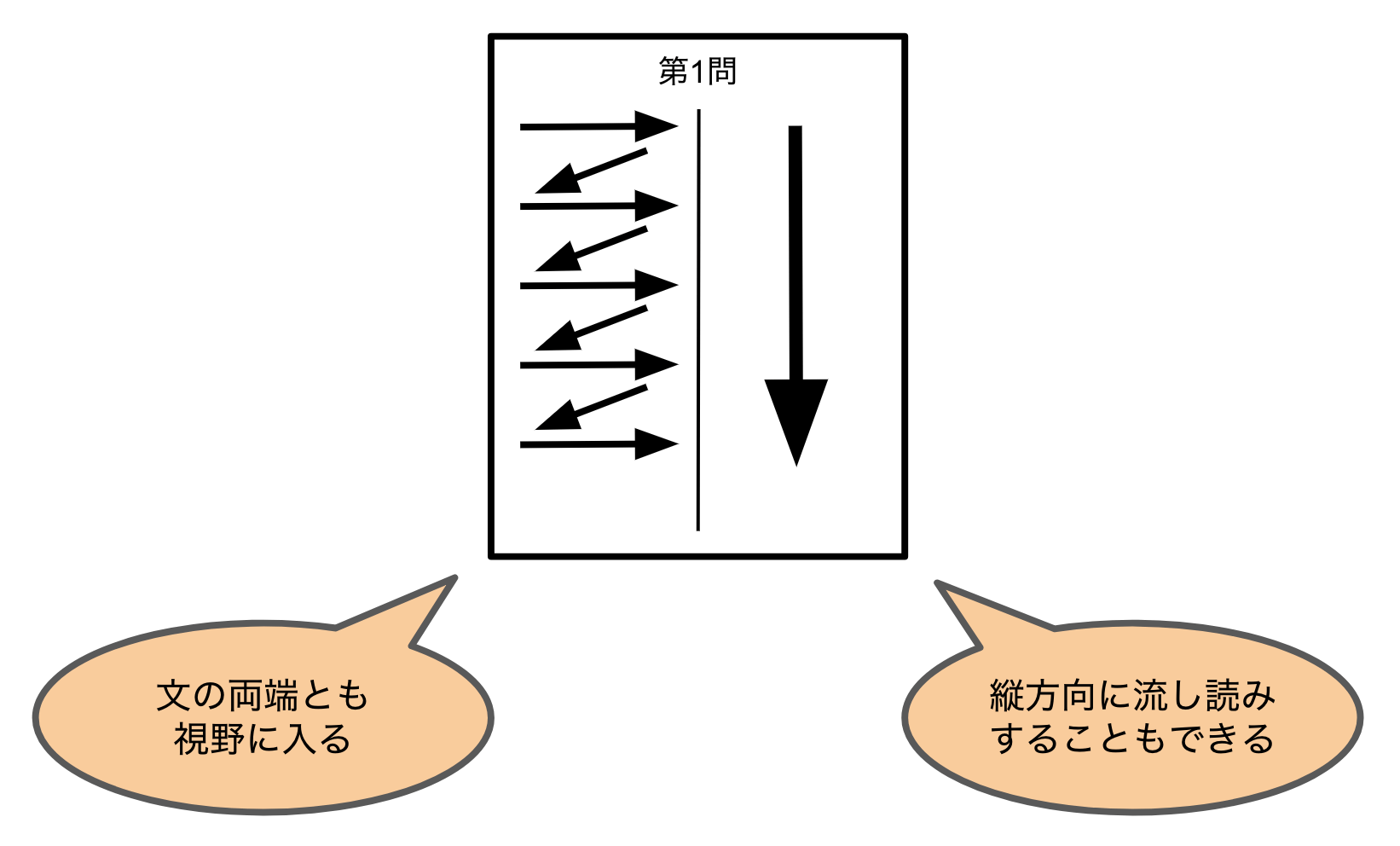

以上から、解答用紙を真ん中で分けることをオススメします。
文章や図の配置は、普段スマホで眺めているサイトと同様にすれば大丈夫です。


















コメントを残す